How to use integral method in kinetics 1
How to use integral method in kinetics 1
Table of Contents
Introduction
Understanding how to use integral method in kinetics 1 for zeroth order reaction is essential for anyone venturing into the world of chemistry, and mastering the integral method is a key component of that understanding. In this blog post, we will explore the integral method’s role in analyzing reaction rates, which is crucial for predicting how different conditions affect the speed of chemical reactions.
With the help of myetutors, we aim to break down complex concepts into manageable steps, guiding you through the mathematical applications and real-world implications of the integral method in kinetics.
Whether you’re a student seeking clarity for your coursework or just looking to enhance your knowledge, this comprehensive guide will empower you to utilize the integral method with confidence and precision.
Zeroth Order Reaction
Fascinatingly, how to use integral method in kinetics 1 for a zeroth order reaction serves somewhat obscurely as foundational building block deep within complex reaction rates dynamics. Dealing with zeroth order reactions requires understanding that reaction rate remains constant regardless of reactant concentration levels somehow.
Reaction proceeds at same rate regardless of reactant amount until completion is reached. Mathematically speaking a zeroth order reaction’s dynamics are succinctly captured via an integral approach. Rate law gets expressed as rate equals negative change in reactants over time equals k where k somehow represents a constant value.
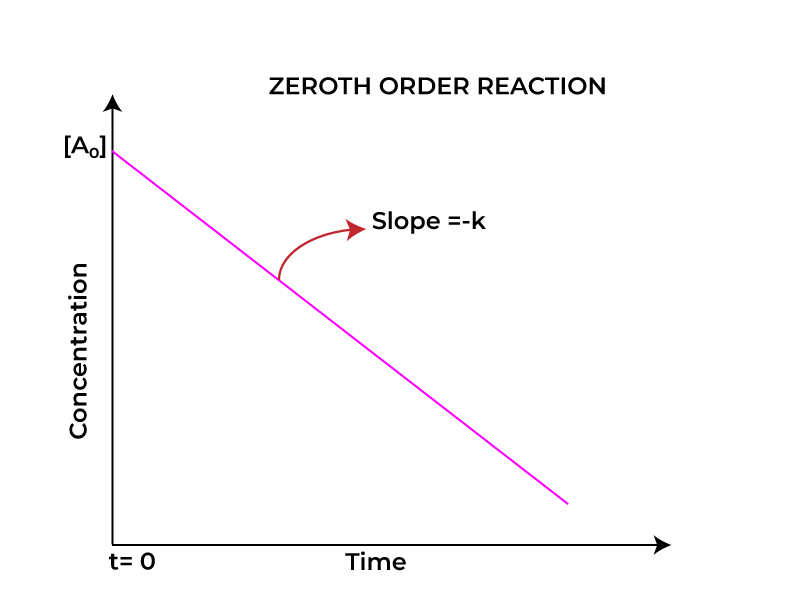
Solving this equation yields a simple linear relationship [A] = [A0] – kt where [A0] represents initial reactant concentration and t denotes time. This equation shows concentration of reactant decreases linearly over time rather than exponentially like first order reactions occur suddenly.
Plotting reactant concentration against time yields a straight line with slope of -k somewhat rapidly under zeroth order kinetics. Chemists find it easier under most circumstances to characterize reaction behavior in complex environments without unnecessary complications.
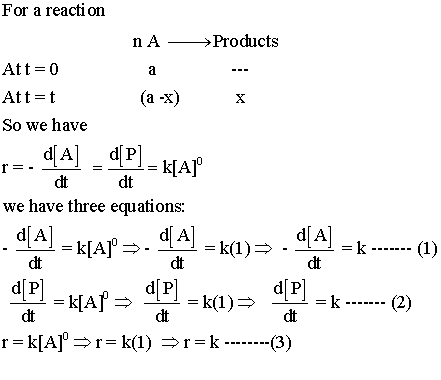
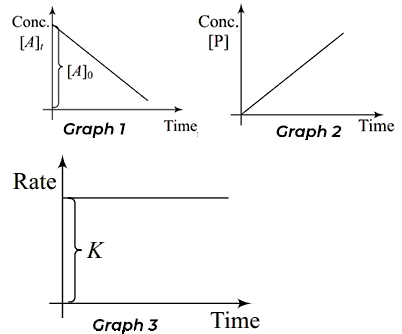
How to use integral method in kinetics 1 for zeroth order reaction, it’s essential to visualize the data, and that’s where zeroth-order reaction graphs come into play.
In graph 1, A zeroth-order reaction is characterized by a constant reaction rate that remains unaffected by the concentration of the reactants.
This unique property allows us to plot a straightforward graph where the concentration of the reactant, [A], is graphed against time (t). In the case of a zeroth-order reaction, you’ll notice that the graph is linear, showcasing a decrease in concentration at a constant rate. The slope of this line, represented as -k (where k is the rate constant), indicates the rate at which the reactant is being consumed.
In graph 2, A zeroth-order reaction is characterized by a constant reaction rate that remains unaffected by the concentration of the reactants.
This unique property allows us to plot a straightforward graph where the concentration of the products, [P], is graphed against time (t). In the case of a zeroth-order reaction, you’ll notice that the graph is linear, showcasing a increase in concentration at a constant rate. The slope of this line, represented as k (where k is the rate constant), indicates the rate at which the reactant is being formed.
In graph 3, A zeroth-order reaction is characterized by a constant reaction rate that remains unaffected by the concentration of the reactants.
This unique property allows us to plot a straightforward graph where the rate of reaction (r), is graphed against time (t). In the case of a zeroth-order reaction, you’ll notice that the graph is straight line parallel to time axis.