How to use integral method in kinetics 2
How to use integral method in kinetics 2
Table of Contents
Introduction
Understanding the intricacies of chemical kinetics is crucial for anyone diving into the world of chemistry, especially when it comes to analyzing the behavior of first-order reactions.
The how to use integral method in kinetics 2, is one of the most effective tools in this realm, allowing you to derive meaningful insights about how concentrations change over time.
Whether you’re a student striving to grasp complex concepts or a seasoned chemist looking to refine your approach, mastering the integral method can elevate your understanding and application of kinetic principles.
In this blog post, how to use integral method in kinetics 2 for first Order reaction, we’ll unravel the steps to effectively use the integral method for first-order reactions, providing you with all the knowledge you need to analyze reaction rates with confidence and clarity. Get ready to transform your kinetics studies into a clear, structured process that demystifies the fascinating world of chemical reactions!
How to use integral method in kinetics
How to use integral method in kinetics 2 for first order reaction is fundamental to grasping how various chemical processes unfold over time. A first-order reaction is defined by its unique characteristic: the rate of reaction is directly proportional to the concentration of one reactant.
This means that as the concentration of that reactant decreases, so does the reaction rate, leading to a predictable and exponential decay in the concentration of products over time. First-order reactions can be represented mathematically by the equation
A → Products
Initial mole a —-
Moles at Equi (a-x) x


Interpretation of graph
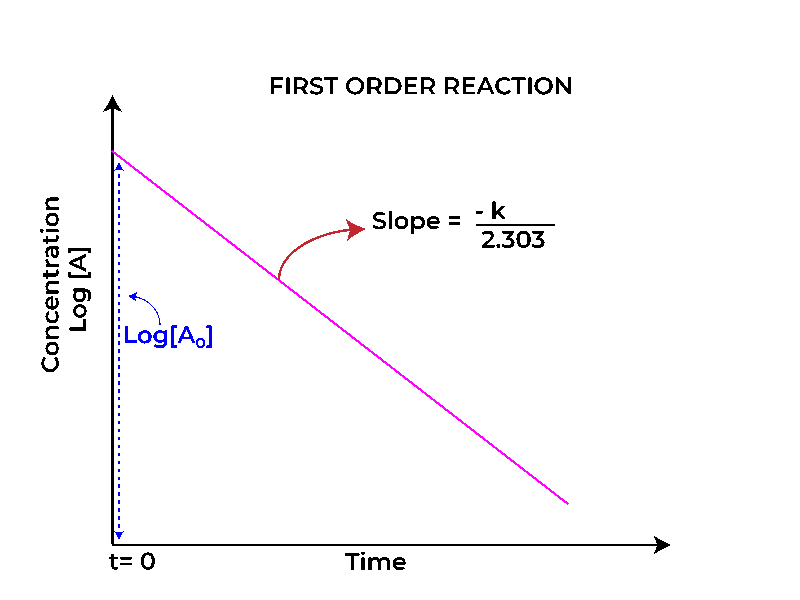
In a first-order reaction, the graph of concentration (C) versus time (t) will yield an exponential decay curve. As time progresses, the concentration of the reactant diminishes, showcasing a smooth, continuous descent towards zero.
This behavior signifies that the rate of reaction is directly proportional to the concentration of the reactant at any given moment. The steeper the curve, the faster the reaction. Importantly, this graph highlights the characteristic feature of first-order kinetics: the concentration decreases rapidly at first but slows down as time goes on, suggesting that the reactant is being depleted.
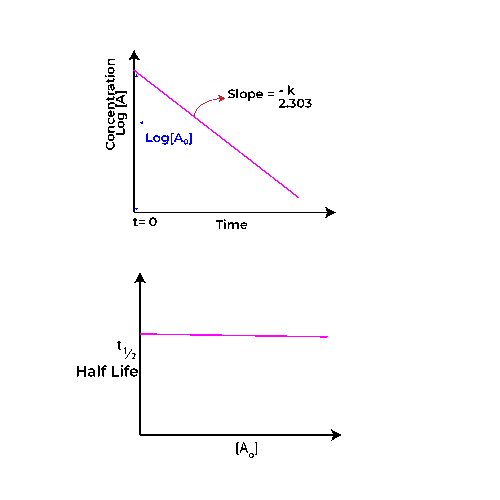
In stark contrast to the concentration graph, the half-life (t₁/₂) against time graph for a first-order reaction reveals a linear relationship. For first-order reactions, the half-life remains constant, regardless of the initial concentration.
This is illustrated by a horizontal line on the graph, indicating that no matter how much of the reactant is present at the beginning, the time taken for half of it to decompose remains the same.
In conclusion, mastering how to use integral method in kinetics 2 for first order reactions is an essential skill for anyone delving into the realm of chemical kinetics.
With myetutors by your side, you’ll find the tools and resources you need to deepen your understanding and excel in your studies. By applying the principles and techniques outlined in our blog post, you can confidently analyze reaction rates, determine concentration changes over time, and utilize this knowledge to tackle complex problems.
Remember, practice is key to mastery, so don’t hesitate to leverage myetutors’ comprehensive learning materials and expert guidance. Thank you for reading, and we wish you the best on your journey toward becoming a kinetics expert!
