Initial rate method know it all faster
Initial rate method know it all faster
Table of Contents
Introduction
In the dynamic world of chemistry, understanding reaction rates is crucial for both students and professionals alike. The Initial rate method know it all faster, in chemical kinetics stands as a pivotal technique that allows us to analyze the speed of chemical reactions right from the start, providing invaluable insights into kinetics and mechanisms.
For those looking to master this essential concept, our comprehensive guide, featuring myetutors, breaks down the intricacies of the initial rate method, unveiling its applications and advantages across various contexts.
Whether you’re a student aiming for academic excellence or a professional seeking to enhance your practical skills, this blog post will equip you with the knowledge and confidence to harness the full potential of the Initial rate method know it all faster method empowering your understanding of chemical processes like never before.
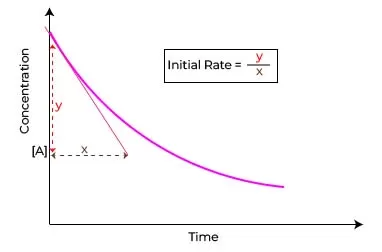
Initial rate method
Specifically, Initial rate method know it all faster, a method focuses on measuring the rate of reaction at its very beginning hence the term “initial rate.” By observing the concentration of reactants or products shortly after a reaction commences, you can ascertain the velocity at which the reaction progresses under specified conditions.
The beauty of the initial rate method lies in its simplicity and efficiency. By using small time intervals immediately after the reaction starts, it minimizes complications that may arise as the reaction approaches equilibrium. This method becomes particularly valuable when dealing with reactions that exhibit varying rates over time or when the formation of products can inhibit the reaction itself.
Practically, the initial rate method can be applied in a multitude of scenarios, including determining reaction orders, evaluating the effects of catalysts, and exploring temperature influences.
For instance, in a common scenario, one might measure how quickly a colored product forms in a reaction by taking discrete measurements of absorbance at the beginning of the reaction. Statistical analysis of these initial rates can then lead to profound conclusions about the underlying chemical processes at play.
Employing the initial rate method is an indispensable skill for anyone delving into the field of kinetics via platforms like myetutors, as it equips students and professionals alike with the tools necessary to unravel the dynamic nature of chemical reactions with accuracy and depth.
Numerical
For a hypothetical reaction
2 A + 2B → C + D
The rate data was collected at 313 K for the reaction
| S. No. | Experiment | [A] mol L-1 | [B] mol L-1 | Initial Rate of D Mol L-1s-1 |
| 1 | I | 0.1 | 0.1 | 6.0 x 10-3 |
| 2 | II | 0.3 | 0.2 | 7.2 x 10-3 |
| 3 | III | 0.3 | 0.4 | 2.88 x 10-1 |
| 4 | IV | 0.4 | 0.1 | 2.4 x 10-2 |
Calculate
- Rate Law expression
- Order of reaction
- Units for the rate constant
- Rate of reaction when [A] = 0.5 mol L-1 and [B] = 0.2 mol L-1
Answer:
Rate Law using initial rate data requires a set of date of experiments and which is solved to get rate law expression
The hypothetical rate law for the reaction is ⇒ r = K [A]x[B]y
Substituting the values of r, A, and B we get four equation
6.0 x 10-3 = K [0.1]x[0.1]y ——— (i)
7..2 x 10-3 = K [0.3]x[0.2]y ———(ii)
2.88 x 10-1 = K [0.3]x[0.4]y ——–(iii)
2.4 x 10-2 = K [0.4]x[0.1]y ——— (iv)
Now taking ratios of (ii) and (iii)
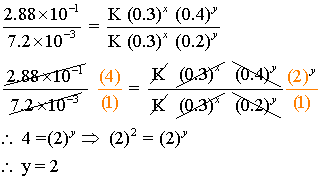
Similarly, we can calculate for x by taking the ratio of (i), and (iv)
x =1
Thus rate Law expression is r = K [A]1[B]2
Thus the order of the reaction is 3rd order
The units for the rate constant are
K= Mol-2 L2 s-1
For calculating rate constant
substitute values of x and y in equation (i), we get
6.0 x 10-3 = K [0.1]1[0.1]2
Solving the equation for K we get
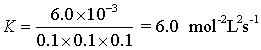
The rate of reaction for given concentrations is
r = 6.0 x (0.5)1 x (0.2)2
rate of reaction (r) = 0.12 mol L-1 s-1
As we wrap up our exploration of the Initial Rate Method and its applications in various fields, it’s clear that mastering this technique can significantly enhance your analytical and problem-solving skills.
Whether you’re diving deep into reaction kinetics, optimizing processes, or exploring new methodologies, the insights gained from utilizing the Initial Rate Method can provide you with a competitive edge. We encourage you to experiment with this method in your academic or professional pursuits, and remember that continuous practice will solidify your understanding.
For those looking to delve deeper into this topic or seeking personalized guidance, myetutors is here to support you every step of the way. Thank you for reading, and happy learning!

